Verifiable Credentials with JSON-LD and BBS+ Signatures
Main
- [Working Draft] Verifiable Credential Data Integrity 1.0 2023-09-02 - Securing the Integrity of Verifiable Credential Data
This specification describes mechanisms for ensuring the authenticity and integrity of Verifiable Credentials and similar types of constrained digital documents using cryptography, especially through the use of digital signatures and related mathematical proofs. Cryptographic proofs enable functionality that is useful to implementors of distributed systems.
About
- Verifiable Credentials Flavors Explained 2021 CCI Kaliya ‘Identity Woman’ Young Presentation
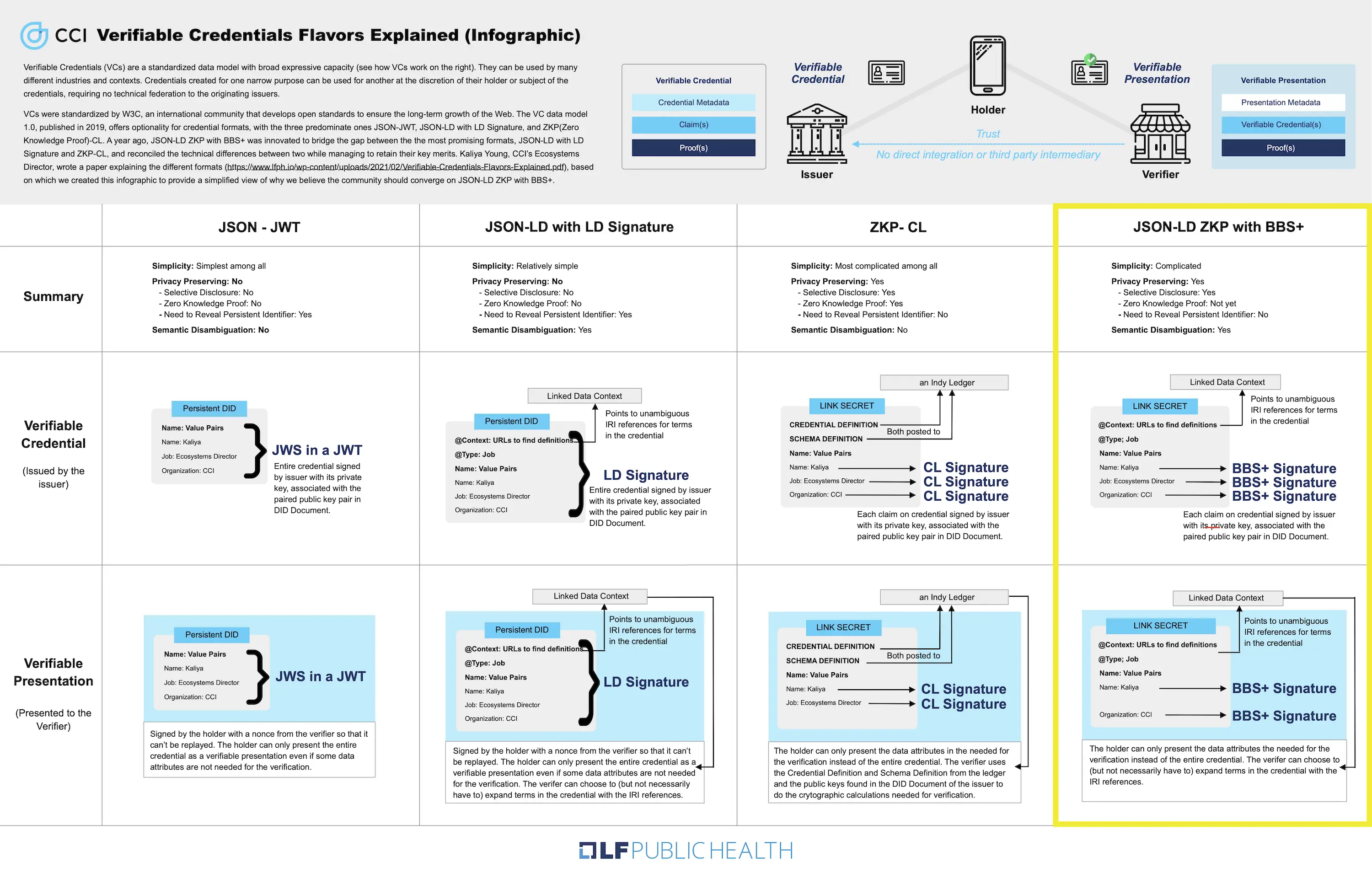
This approach to VCs is innovative because it brings together different elements from several of the existing approaches to VCs. It is based on the usage of BBS+ JSON-LD Signatures, which is a subclass of LD Signatures, in combination with a JSON-LD credential schema. The cryptography behind this mechanism is BBS+ Signatures, which require what’s called a pairing-friendly curve. Existing implementations in the VC ecosystem use the elliptic curve BLS12–381
- BBS+, JSON-LD and Interoperability of Verifiable Credentials 2021-06-20 Coinmonks
In order to request attributes from the credentials JSON-LD frames are used. The credentials and the proofs created by BBS+ signatures are self-describing and do not require a ledger(unlike CL signature based systems like Hyperledger Indy).
- [Working Draft] BBS Cryptosuite v2023 - Securing Verifiable Credentials with Selective Disclosure using BBS Signatures 2023-05-24 W3C
This specification defines a set of cryptographic suites for the purpose of creating, verifying and deriving proofs for BBS+ Signatures in conformance with the Data Integrity [VC-DATA-INTEGRITY] specification.
In general the suites uses the RDF Dataset Normalization Algorithm [RDF-DATASET-NORMALIZATION] to transform an input document into its canonical form. It then uses the statement digest algorithm to digest each statement to be signed individually, finally the digested statements are signed using the defined signature algorithm.
BBS+ signatures [CFRG-BBS-SIGNATURE] are compatible with any pairing friendly elliptic curve, however the cryptographic suites defined in this document elect to only allow the usage of the BLS12-381 for interoperability purposes.
- [Literature] Revisiting BBS Signatures 2023, Stefano Tessaro and Chenzhi Zhu
BBS signatures were implicitly proposed by Boneh, Boyen, and Shacham (CRYPTO ’04) as part of their group signature scheme, and explicitly cast as stand-alone signatures by Camenisch and Lysyanskaya (CRYPTO ’04). A provably secure version, called BBS+, was then devised by Au, Susilo, and Mu (SCN ’06), and is currently the object of a standardization effort which has led to a recent RFC draft. BBS+ signatures are suitable for use within anonymous credential and DAA systems, as their algebraic structure enables efficient proofs of knowledge of message-signature pairs that support partial disclosure.
BBS+ signatures consist of one group element and two scalars. As our first contribution, we prove that a variant of BBS+ producing shorter signatures, consisting only of one group element and one scalar, is also secure. The resulting scheme is essentially the original BBS proposal, which was lacking a proof of security. Here we show it satisfies, under the q-SDH assumption, the same provable security guarantees as BBS+. We also provide a complementary tight analysis in the algebraic group model, which heuristically justifies instantiations with potentially shorter signatures.
- [JWT; BBS+; Data Integrity] Formalising Linked-Data based Verifiable Credentials for Selective Disclosure 2022 Dan Yamamoto, Yuji Suga, Kazue Sako IEEE

- SSI Essentials: Zero Knowledge Proof (ZKP) and Selective Disclosure, till death do us part? 2022-01-23 Gataca
Selective disclosure via BBS+ signatures […]
Like monoclaim credentials allow users to share specific claims from a VC, BBS+ Signatures is a multi-message digital signature scheme (named after its creators Boneh, Boyen, and Shacham) that gives users the possibility of sharing VCs with only specific attributes revealed. How does it work?
BBS+ signatures allow a VC holder to derive proofs from the original signature:
- Deriving a proof: When a holder takes the signed VC and hides one, several, or none of the containing claims, creating a new signature (a derived proof) using the Issuer’s public key. This derived proof can prove that the holder knows all of the original claims contained in the VC but chooses only to reveal the required ones.
- Verifying a proof: The verifier validates the derived proof using the Issuer’s public key. This process enables the verifier to confirm the validity of the proof, proving that the subset of claims was part of an original message signed by the Issuer.
- Why the Verifiable Credentials Community Should Converge on BBS+ 2021-03-24 Evernym
BBS+ LD-Proofs use JSON-LD schemas, so credentials that use them can have a rich, hierarchical set of attributes. Instead of the heavy-handed mechanism for the encoding and canonicalization of attributes values that we’d imagined for Rich Schemas, they use RDF canonicalization and a hash function. Rather than expanding the credential definition, they discarded it, taking advantage of some properties of BBS+ keys which allow for deterministic expansion.
Development
- [Code] jsonld-signatures-bbs 2022-12-18 Mattr Global, NPMJS
The following repository contains a linked data proof implementation for creating BBS+ Signatures using BLS12-381 key pairs.
Due to the properties of a BBS+ Signatures, zero knowledge proof can be derived from the signature, where-by the party generating the proof can elect to selectively disclose statements from the originally signed payload.
- [GitHub] bbs-signatures 2022-12-21 Mattr Global
BBS+ Signatures are a digital signature algorithm originally born from the work on Short group signatures by Boneh, Boyen, and Shachum which was later improved on in Constant-Size Dynamic k-TAA as BBS+ and touched on again in section 4.3 in Anonymous Attestation Using the Strong Diffie Hellman Assumption Revisited .
BBS+ signatures require a pairing-friendly curve, this library includes support for BLS12-381.
BBS+ Signatures allow for multi-message signing whilst producing a single output signature. With a BBS signature, a proof of knowledge based proof can be produced where only some of the originally signed messages are revealed at the discretion of the prover.
- [GitHub] jsonld-signatures-bbs Mattr Global
The following repository contains a linked data proof implementation for creating BBS+ Signatures using BLS12-381 key pairs.
Due to the properties of a BBS+ Signatures, zero knowledge proof can be derived from the signature, where-by the party generating the proof can elect to selectively disclose statements from the originally signed payload.
This library is runnable in browser and Node.js through the WASM based crypto implementation provided by bbs-signatures. Note bbs-signatures also has an optional dependency on node-bbs-signatures which can be used when running in Node.JS environments to obtain better performance. For environments that do not feature WASM support such as react native, bbs-signatures includes an automatic roll back to an asm.js version but note however the performance difference between asm.js and WASM is significant, for those inclined there are runnable benchmarks in bbs-signatures.
- [GitHub] jsonld-signatures-bbs 2023-02-23 ZKP-LD
Experimental: do not use in production
- Based on MATTR’s jsonld-signatures-bbs
- Supports termwise selective disclosure, proof of termwise equality, and credential aggregation
- dependencies upgraded
- WASM only; Neon is currently not supported
- [GitHub] bbs-signatures ZKP-LD
Experimental: do not use in production
- Based on MATTR’s bbs-signatures
- Supports termwise selective disclosure, proof of termwise equality, and credential aggregation
- WASM only; Neon is currently not supported
- Implement Compound Proof BBS+ verifiable credentials using ASP.NET Core and MATTR 2021-12-13 damienbod
This article shows how Zero Knowledge Proofs BBS+ verifiable credentials can be used to verify credential subject data from two separate verifiable credentials implemented in ASP.NET Core and MATTR. The ZKP BBS+ verifiable credentials are issued and stored on a digital wallet using a Self-Issued Identity Provider (SIOP) and OpenID Connect. A compound proof presentation template is created to verify the user data in a single verify.
Code: https://github.com/swiss-ssi-group/MattrAspNetCoreCompoundProofBBS
Blum Blum Shub
- Blum Blum Shub A Security Site
Blum Blum Shub (BBS) is used as a pseudo-random number generator (it is pseudo as it is not a truly random number, and where its randomisation depends on a random seed). It was created by Lenore Blum, Manuel Blum and Michael Shub in 1968. Blum Blum Shub uses the form of xn+1=x2n(modM), and where x0 is a random seed. The value of M is equal to pq, and where p and q are prime numbers. These values of p and q are both congruent to 3 mod 4 (p=q=3(mod4)). The security of the method involves the difficulty in factorizing M. It is slow, but is the strongest proven random number generator. For each step, we extract some of the information from xn+1, and which is typically the least significant bit. It would not be used within a cipher application, but could be used in key generation.
- A SIMPLE UNPREDICTABLE PSEUDO-RANDOM NUMBER GENERATOR 1986 L. BLUM?, M. BLUM AND M. SHUB SIAM
What do we want from a pseudo-random sequence generator? Ideally, we would like a pseudo-random sequence generator to quickly produce, from short seeds, long sequences (of bits) that appear in every way to be generated by successive flips of a fair coin.
Certainly, the idea of a (fast) deterministic mechanism producing such non-deterministic behavior seems contradictory: by observing its outcome over time, we could in principle eventually detect the determinism and simulate such a generator.
- [Python] Blum Blum Shub PRNG algorithm GKBRK
The algorithm is very short and simple. Starting from the seed, the next state can be computed by passing the current state through the following formula.
f(x) = x2 mod MIn this formula, M is the product of p and q, two large primes.
The complexity in this algorithm is hidden in the parameters; the seed and the modulus M. In order to have a long cycle length and fulfill its security promises, Blum Blum Shub has a few constraints on its parameters.
In contrast, some more complex PRNG algorithms can work with pretty much any randomized seed.